Originally published on Medium - January 20, 2022

Lately when I was coding I tried to compare two float numbers in Python and in my eyes those two numbers were the same but it returned false and this was new to me as I don’t work with floats and if I do most of the time I don’t care about their precision so I started to ask “why is it returning false?” Here is what I found.

Inspired by Fred Baptiste

Binary Representation

As we all know computers use Binary numbers which is a base 2 system and float numbers can be represented using fractions, means that 0.1 can be represented as 1 ÷ 10 where 1 is the dividend and 10 is the divisor.

If we try to write 1 ÷ 10 in binary it will be (1 ÷ 1010)₂ which will result in an infinite amount of numbers in the binary system. The figure below will demonstrate how that mathematical operation in the binary system will result in infinite numbers.

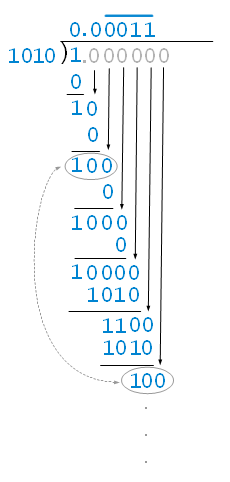
As you can see this operation will keep going infinitely and computers cannot store infinite numbers because it will take infinite space.

How Computers Handle This

So computers use a close number to that so it can be stored in the memory. What I mean is that rather than storing 0.1 the computer may store 0.10000000000000001 which when you look at it may say it’s not that big an amount to worry about but the issue is that 0.1 is not equal to 0.10000000000000001.

Also when we do operations like 0.1 + 0.1 + 0.1 the result is not 0.3. Look at the example below.

1
2
3
4
5
6
7
8

a = 0.1
b = 0.1 + 0.1 + 0.1
c = 0.3

print(f"{a:.20f}")  # 0.10000000000000000555
print(f"{b:.20f}")  # 0.30000000000000004441
print(f"{c:.20f}")  # 0.29999999999999998890
print(b == c)       # False

As you can see in this example the variable a was initialized to 0.1 but if we print with more than 16 digits we’ll get some random numbers and so with the other variables.

An important thing to note is that variable b will not equal to c.

Some people use rounding method to get around this issue but it doesn’t solve it as a whole. Some other people try to limit digits to 1 decimal point but in the computer’s memory this 0.1 will always equal to some number close to that but not it.

This issue can cause big trouble in the financial industry because the precision of a number matters to them. They’re dealing with money which if they use floats can cause big losses.

Is Close Method

Using absolute and relative tolerance, there are some ways that define how precise you want the float number to be close to the real number. The most known ways are called absolute and relative tolerance.

Absolute Tolerance

Absolute tolerance is defining how many digits the two numbers should be close to each other. Example: you can say if number X and number Y are within 0.001 and how this works is you subtract X - Y and then compare the result to be less than 0.001. Look at the example below to demonstrate how this works.

1
2
3
4
5
6
7
8

a = 0.1
b = 0.10001
tolerance = 0.000001

if abs(a - b) < tolerance:
    print("True")
else:
    print("False")

As you can see we defined a 0.000001 range so if a - b is less than that number it will print True and this method works very well for very small numbers. If we try to use this with big numbers like 5000.1 and 5000.2 these numbers in our eyes are so close but if we try to use absolute tolerance it will return false because 5000.2 - 5000.1 will be greater than 0.00001 and this is the problem with absolute tolerance.

Relative Tolerance

Relative tolerance solves the problem that absolute tolerance has with larger numbers. Instead of using a fixed difference, it uses a percentage of the numbers being compared.

The way it works is you calculate the relative difference between two numbers. For example if you have numbers X and Y, you calculate |X - Y| / max(|X|, |Y|) and compare that to your tolerance.

This means for large numbers like 5000.1 and 5000.2, the relative difference is tiny even though the absolute difference is 0.1. And for small numbers like 0.0001 and 0.0002, the relative difference is large which is what we want.

Python has a built-in function called math.isclose() that uses both absolute and relative tolerance which makes comparing floats much easier. You can specify both tolerances or just use the defaults.

1
2
3
4
5
6
7

import math

a = 5000.0001
b = 5000.0002

# Using relative tolerance
print(math.isclose(a, b, rel_tol=0.001))  # True

Conclusion

So to summarize, floats are not precise because computers store them in binary and some decimal numbers cannot be represented exactly in binary without infinite digits. The computer has to round them which causes precision errors.

If you’re working with floats and need to compare them, don’t use ==. Instead use tolerance methods like math.isclose() or if you’re dealing with money, use decimal types like Python’s Decimal class which handles decimal numbers more accurately.

This was something I didn’t know before and it made me realize how important it is to understand what’s happening under the hood when you’re writing code.